Example 1: Amount of Degrees
求给定区间[X, Y]中满足下列条件的整数个数：这个数恰好等于K个互不相等的B的整数次幂的和。其中 2 <= B <= 10。 如指定[15, 20]，K=2，B=2，有三个数满足：
17=2^4+2^0 18=2^4+2^1 20=2^4+2^2 因此输出 3
原题在这
此题只需求[0, Y]和[0, X - 1]的解，然后相减即可；
可以看出满足条件的数其实是一个B进制的表示，且系数只能为0或1。
对于2进制，相当于求某些数字的二进制表示上，有K个位为1，这样的数的个数;
例如n=13,k=3时，13（1101）有4位，即在下面的01树的第4层（根为第0层）找出整条路径有3个1的路径总数；
但实际上有些数满足条件但比13大，比如14（1110），因此还需做其他的处理。
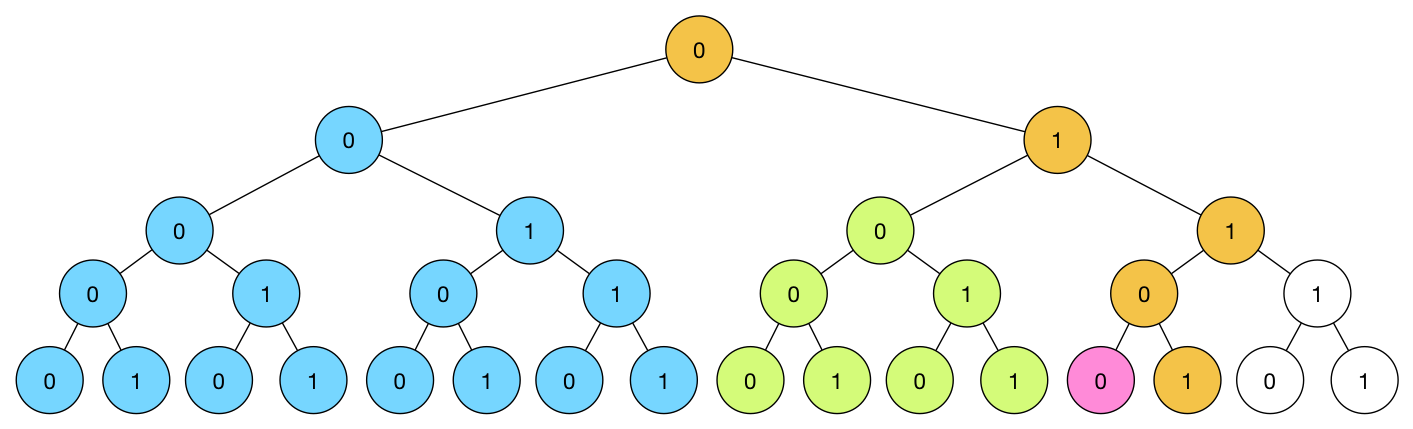设一个2维数组，dp[i][j]，表示一个i位的2进制数（其实更应该理解为一个长度为i的01串）中，有j位为1的数的个数，则
初始时有：dp[0][0] = 1, dp[0][1] = 0;
第i层至多有i个1，即j<=i;
dp[i][j] = dp[i - 1][j] + dp[i - 1][j - 1]; // 已有的i-1位有j个1，第i位为0，或已有的i-1位有j-1个1，再来一个1
对于进制大于2，由于要求系数为0或1，所以可以转化为2进制；
实际上，当某个数的k进制中有一位的系数大于1，则只需将这一位极其第位全置为1即可（这样就是小于等于原数的最大的满足条件的数）
vector<vector<int>> dp(33, vector<int>(33, 0));
void init() {
dp[0][0] = 1;
for (int i = 1; i <= 32; i++) {
dp[i][0] = dp[i - 1][0];
for (int j = 1; j <= i; j++) {
dp[i][j] = dp[i - 1][j] + dp[i - 1][j - 1];
}
}
}
int amountOfDegrees(int n, int b, int k) {
int bits = 0;
vector<int> coe;
while (n) {
coe.push_back(n % b);
n /= b;
bits++;
}
int count = 0;
int ans = 0;
for (int i = bits - 1; i >= 0; i--) {
if (coe[i] > 1) {
ans += dp[i + 1][k - count];
} else if (coe[i] == 1) {
ans += dp[i][k - count];
if (++count == k) break;
}
}
if (count == k) ans++;
return ans;
}Example 2: 不要62
不吉利的数字为所有含有4或62的号码，统计区间内不含4和62的数字个数。0<n<=m<1000000
原题
int dp[10][10]; // dp[i][j]表示一个i位的数且最高位是j时满足条件的数的个数
int bits[10]; // 给定数的每一位
void init() {
for (int i = 1; i < 7; i++) { // 枚举所有位数
for (int j = 0; j <= 9; j++) { // 枚举最高位可能的数字
if (i == 1 && j != 4) {
dp[i][j] = 1;
continue;
}
}
for (int k = 0; k <= 9; k++) { // 枚举次高位可能的数字
if (j != 4 && k != 4 && !(j == 6 && k == 2)) {
dp[i][j] += dp[i - 1][k];
}
}
}
}
}
int solve(int n) {
if (n == 0) return 1;
int len = 0;
while (n) {
bits[len++] = n % 10;
n /= 10;
}
bits[len] = 0;
int ans = 0;
for (int i = len - 1; i >= 0; i--) {
for (int j = 0; j < bits[i]; j++) {
if (j != 4 && !(j == 2 && bits[i + 1] == 6))
// 这里相当于固定第i位以及更高位上面的数字为n对应位的数字（位数超过len就当成是0），
// 且比i小的位上从0到9枚举（当然要满足条件）。
// 这样就导致最低位没有枚举到n的最低位的数，
// 也就是说solve()没有考虑n是否满足条件，其计算的是[0,n)范围的结果
ans += dp[i + 1][j];
}
// 如果被固定为n对应位的第i位不满足条件，就直接跳出
if (bits[i] == 4 || (bits[i] == 2 && bits[i + 1] == 6)) break;
}
return ans;
}
int main() {
init();
int m, n;
while (cin >> m >> n) {
if (m == 0 && n == 0) break;
// 注意solve()没有判断n是否满足
cout << solve(n + 1) - solve(m) << endl;
}
return 0;
}Example 3: B-number
求小等于n是13的倍数且含有’13’的数的个数 原题
比上一个例子复杂一点，主要是dp里要包含两个状态，因此定义dp[i][j][l][k]为：
共有i位的、最高位为j、%13等于l、是否包含’13’的状态为k(k=1或2)的数字的个数
这里有一个公式：如果 k % m = l, (a * b + k) % m = ll 则
ll = (l + (a * b) % m) % m
#include <iostream>
#include <vector>
using namespace std;
int dp[11][10][13][2];
int bits[11];
void init() {
int shi = 1;
for (int i = 1; i < 11; i++) {
for (int j = 0; j < 10; j++) {
for (int k = 0; k < 10; k++) {
for (int l = 0; l < 13; l++) {
if (i == 1 && j == l) {
dp[1][j][l][0] = 1;
continue;
}
int ll = (l + (j * shi) % 13) % 13;
if (j == 1 && k == 3) {
dp[i][j][ll][1] += dp[i - 1][k][l][0];
} else {
dp[i][j][ll][0] += dp[i - 1][k][l][0];
}
dp[i][j][ll][1] += dp[i - 1][k][l][1];
}
}
}
shi *= 10;
}
}
int solve(int n) {
int len = 0;
int shi = 1;
int nn = n;
while (n) {
bits[len++] = n % 10;
n /= 10;
shi *= 10;
}
bits[len] = 0;
int ans = 0;
bool has = false;
for (int i = len - 1; i >= 0; i--) {
for (int j = 0; j < bits[i]; j++) {
// 这里相当于i前面的位固定为n对应位的数，因此取的余数应该是算上前面固定位的数后，余数为0，
// 所以实际取的l不应该是0。
int l = (13 - (nn / shi * shi) % 13) % 13;
ans += dp[i + 1][j][l][1];
// 如果i位和前一位为13，则...
if (has || bits[i + 1] == 1 && j == 3)
ans += dp[i + 1][j][l][0];
int bb = 0;
}
// 如果前面已经被固定的位中出现了13，则...
if (bits[i] == 3 && bits[i + 1] == 1) has = true;
shi /= 10;
}
return ans;
}
int main() {
init();
int m;
while (cin >> m && m) {
cout << solve(m + 1) << endl;
}
return 0;
}